Navigazione di servizio
Ricerca
Metodi utilizzati
Secondo la teoria dei valori estremi i valori più grandi di una quantità (per esempio precipitazioni giornaliere o raffiche su 1s), presi ciascuno da intervalli di lunghezza uguale, possono essere utilizzati per dedurre il comportamento estremo di questa quantità, quindi a livelli al di sopra di quelli che sono stati osservati. La distribuzione di questi massimi si chiama “distribuzione generalizzata dei valori estremi” (Generalized Extreme Value distribution in inglese), abbreviata di seguito con GEV. Di conseguenza, le osservazioni utilizzate per l’analisi dei valori estremi in questo portale web sono massimi stagionali e/o annuali.
I livelli di ritorno sono stimati con l’approccio denominato inferenza bayesiana. Il vantaggio di questo approccio è che prende in conto le incertezze in modo esplicito.
Viene stimato un insieme di distribuzioni GEV tutte compatibili con le osservazioni. Nella pratica questo insieme consiste in un grande numero di distribuzioni simulate, per esempio mille, ciascuna delle quali fornisce una stima del livello di ritorno.
Per un periodo di ritorno particolare otteniamo di conseguenza non uno livello di ritorno, ma una distribuzione di livelli di ritorno. Per ogni periodo di ritorno sul diagramma dei livelli di ritorno (quindi per ogni posizione sull’ascissa) il livello di ritorno rappresentato (il punto corrispondente sulla linea blu) è la mediana dei livelli di ritorno calcolati per questo periodo di ritorno particolare a partire da tutte le distribuzioni GEV stimate.
Una conseguenza importante di questa procedura è che la linea blu rappresentata sul diagramma dei livelli di ritorno non è più una distribuzione GEV. Tuttavia, come di solito, per un dato periodo di ritorno (per esempio 50 anni), il valore della curva blu in questo punto (per esempio 80mm/giorno) può essere interpretata come la quantità di precipitazioni superata solo all’incirca 20 volte in 1000 anni (in presenza dello stesso clima).
Un grande vantaggio dell’inferenza bayesiana è l’interpretazione intuitiva degli intervalli di confidenza: vi è il 95% di probabilità che il vero livello di ritorno si trovi fra i limiti dell’intervallo di confidenza del 95%.
Quando applichiamo la teoria dei valori estremi ai massimi annuali, supponiamo implicitamente che i processi che portano alle precipitazioni rimangano invariati tutto l’anno. Ovviamente, questo non è sempre il caso: i processi delle precipitazioni dipendono spesso dalla stagione. Utilizzando i massimi annuali per stimare i livelli di ritorno, è di conseguenza possibile che non rispettiamo le condizioni necessarie per ottenere una stima affidabile.
Per evitare questo problema, stimiamo prima i livelli di ritorno stagione per stagione, utilizzando i massimi stagionali, e poi deriviamo numericamente i livelli di ritorno annuali a partire dai livelli di ritorno stagionali.
I diagrammi di frequenza mostrano la probabilità che un dato valore sia superato. La probabilità è espressa sotto forma di periodi di ritorno. Un valore che in un determinato anno ha la probabilità dell’1% di essere superato, secondo le previsioni verrebbe quindi – a lunga scadenza – superato una volta ogni 100 anni. Questo valore, rispettivamente il “valore di ritorno”, ha pertanto un “periodo di ritorno” di 100 anni. In questo caso si parla di un evento che si verifica in media ogni cento anni. I valori di ritorno sono di fatto quantili estremi: la probabilità che il valore di ritorno di 100 anni non sia superato, ammonta allo 0,99. Esso corrisponde perciò al quantile convenzionale di 0,99 (per approfondire il tema si vedano le informazioni complementari).
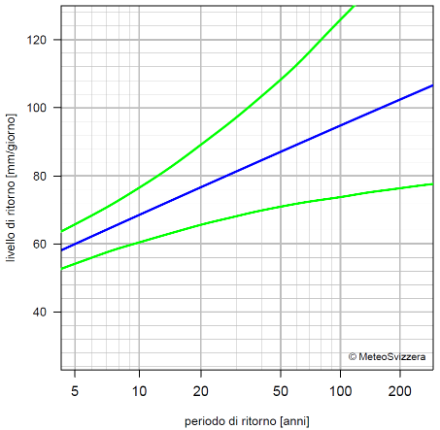
Per richiamare l’attenzione sul comportamento degli eventi più rari, i periodi di ritorno sono trasformati in modo che il rapporto con i valori di ritorno possa essere rappresentato tramite una linea retta al fine di ottenere una distribuzione Gumbel dei massimi annuali (cfr. rapporto).
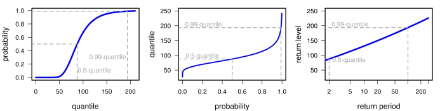
Il diagramma di frequenza riassume il comportamento dei valori estremi. Una serie di valori delle precipitazioni su 1 giorno (asse Y) è messa in relazione con le sue probabilità di superamento, espresse sotto forma di periodi di ritorno (asse X).
Il comportamento estremo delle precipitazioni giornaliere nella stazione di Genève-Cointrin può essere illustrato con il diagramma di frequenza: il valore di ritorno stimato (linea blu) ha una leggera curvatura negativa. Questo indica che esiste un determinato cumulo giornaliero delle precipitazioni, la cui probabilità di superamento è nulla. La curvatura fortemente positiva della linea verde che delimita l’intervallo di confidenza verso l’alto indica invece che questo comportamento estremo è caratterizzato da un alto grado di incertezza: a partire da un determinato cumulo giornaliero delle precipitazioni la probabilità che esso sia superato e che questa probabilità diminuisca piuttosto lentamente (in maniera polinomiale) può anche essere diversa da zero. Ciò comporta, che gli eventi ad alto impatto sul territorio possono avere una probabilità non trascurabile di essere superati.

La serie temporale dei massimi annuali (grafico a sinistra) fornisce una visione d’insieme dei dati mancanti o delle tendenze e dei possibili cicli presenti nella serie. In questo caso le variazioni dei massimi annuali possono essersi verificate in modo assolutamente casuale. L’istogramma (secondo grafico da sinistra) mostra la frequenza con la quale si sono osservati i massimi annuali e può essere interpretato come funzione della densità di probabilità (Probability Density Function PDF) empirica.
Il diagramma dei quantili (secondo grafico da destra, Q-Q plot) aiuta a stabilire se la qualità della stima è affidabile: se il modello risultasse adeguato ai dati disponibili, i quantili empirici dei dati dovrebbero coincidere approssimativamente con i quantili stimati (maggiore è il campione, migliore è il grado di concordanza). In questo caso i punti si situerebbero all’incirca sulla diagonale. Se i quantili empirici superiori fossero invece sistematicamente inferiori ai quantili adattati, ciò indicherebbe che la “coda” della distribuzione effettiva potrebbe diminuire più velocemente di quella della distribuzione adattata. Nella stazione di Genève-Cointrin non è possibile individuare uno scostamento sistematico per difetto o per eccesso della coda delle precipitazioni giornaliere. Le variazioni dei punti attorno alla linea rossa potrebbero presumibilmente essere ridotte mediante una modellizzazione esplicita della dipendenza dalle stagioni dei valori estremi delle precipitazioni giornaliere.
Nel diagramma di frequenza (grafico a destra), per ogni anno del periodo analizzato, i valori massimi sono indicati con dei punti, i cosiddetti «plotting points». Il valore di ogni punto sull’asse Y corrisponde al cumulo delle precipitazioni misurate. Poiché il periodo di ritorno effettivo di questi eventi non è tuttavia noto, la posizione sull’asse X è determinata empiricamente dalla grandezza del campione. Per una serie con una lunghezza di 50 anni, si assegna - ad esempio - un periodo di ritorno di circa 50 anni al valore più elevato, un periodo di ritorno di circa 25 anni al secondo valore più elevato e così via. In altre parole non si indica il comportamento locale della grandezza cercata (ad es. precipitazioni giornaliere) della rispettiva stazione, ma solo la grandezza del campione indipendentemente dalla posizione geografica. Tuttavia è possibile trarre alcune conclusioni confrontando la stima empirica (punti neri) con la stima migliore (linea blu, grafico a destra): ogni deviazione importante o sistematica tra la stima empirica e la stima della distribuzione generalizzata dei valori estremi (GEV) indica, previa considerazione degli errori del campione, che il modello è insufficiente.
I risultati dell’analisi dei valori estremi non sono affidabili – cosa fare?
Ogni analisi dei valori estremi è sottoposta a un test di affidabilità e i relativi risultati sono indicati sulla pagina principale. Queste informazioni non valgono per l’incertezza della stima dovuta alla grandezza limitata del campione. Esse descrivono piuttosto la possibilità che le ipotesi su cui si è basata la scelta del modello statistico possano eventualmente essere sbagliate.
Se, ad esempio, l’affidabilità è dubbia, il modello non rappresenta bene i valori estremi osservati. Sono state definite tre classi di affidabilità: insufficiente, dubbia e buona. Nella tabella sottostante è indicato il significato di ogni livello e come comportarsi in ognuno dei tre casi.
Affidabilità delle analisi dei valori estremi
| Affidabilità | Interpretazione | Cosa fare? |
| insufficiente | I valori estremi misurati sono rappresentati male dal modello. | Questo modello statistico non dovrebbe essere utilizzato. Utilizzate piuttosto i maggiori eventi osservati o la stazione con dati affidabili più vicina. |
| poco affidabili | I valori estremi misurati non sono rappresentati bene dal modello. Le ipotesi alla base sono eventualmente state prese in considerazione in maniera inadeguata. | È necessaria una valutazione accurata. Per la decisione utilizzate gli strumenti ausiliari visivi (rapporto, p. 32). Se i punti si situano sulla diagonale, potete procedere come se l’affidabilità fosse buona; altrimenti come se fosse insufficiente. |
| affidabili | I valori estremi misurati sono rappresentati bene dal modello. | Il modello statistico può essere utilizzato senza limitazioni. |
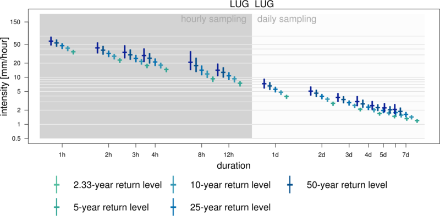
Il grafico delle intensità mostra in un sol colpo d’occhio il comportamento delle precipitazioni molto intense con durate diverse, raffigurato volutamente in modo analogo ai diagrammi di intensità-durata-frequenza (IDF) in uso nell’idrologia, benché il contenuto sia molto diverso: i valori di ritorno qui indicati sono stati stimati separatamente per ogni durata in base ai dati orari delle precipitazioni. Tra le intensità delle precipitazioni con durate diverse non si può presupporre alcun rapporto (cfr. Rapporto tecnico di MeteoSvizzera no. 255 ).
In questo diagramma sia l’asse X sia l’asse Y sono costituiti da una scala logaritmica. Perciò graficamente le differenze nelle intensità minori diventano più grandi, mentre quelle nelle intensità maggiori sembrano più ridotte di quanto lo siano effettivamente. La base logaritmica dell’asse Y mette in evidenza il fatto che l’intensità delle precipitazioni diminuisce tendenzialmente con l’aumentare della durata. Poiché le incertezze sono raffigurate anche sulla scala logaritmica, questa rappresentazione può risultare fuorviante se si confrontano le incertezze, ad esempio valutando la simmetria o l’asimmetria degli intervalli di confidenza dei valori puntuali stimati.
Il colore di fondo indica le diverse osservazioni utilizzate per l’analisi. Le statistiche delle intensità da 1 fino a 12 ore si basano sulle massime annue delle misurazioni ad intervalli fissi con una durata di un’ora (hh:40 - hh+1:40). Le corrispondenti aggregazioni si basano su somme mobili. Per analogia le statistiche delle intensità da 1 a 7 giorni si basano sulle massime annue delle osservazioni giornaliere in un intervallo di tempo fisso (05:40 - 05:40 UTC), aggregate pure con somme mobili.
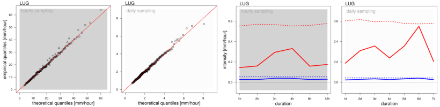
Ci si deve aspettare delle deviazioni casuali dai valori puntuali stimati (linea rossa, a sinistra dell’immagine). Tuttavia queste non dovrebbero formare una struttura o posizionarsi troppo lontano dalla diagonale. Poiché in caso di durate brevi delle precipitazioni i valori dei quantili sono (per costruzione) superiori a quelli in caso di durate lunghe, l’informazione riguardante questi diagrammi dei quantili non è così pertinente come per le analisi dei valori estremi di singoli cumuli di precipitazione. Le informazioni sulla qualità della stima delle intensità da 3 a 12 ore e quelle da 3 a 7 giorni sono quantomeno limitate: in questo esempio si può supporre che l’affidabilità dei valori di ritorno più elevati per le intensità di 3 o 4 ore sia dubbia. Nel complesso non è tuttavia possibile individuare una deviazione sistematica.
I due grafici a destra forniscono informazioni complementari sulla qualità della stima e una valutazione dell’affidabilità dei risultati. Se la linea continua si situa al di sopra della linea tratteggiata, la qualità della stima per questa specifica durata delle precipitazioni è dubbia. La statistica AD si concentra sulla qualità della stima dei valori di ritorno elevati. Se, per quel che riguarda l’errore quadratico medio (RMSE), compaiono esclusivamente deviazioni casuali (ossia se tutti i valori si situano al di sotto della linea blu tratteggiata), ma la statistica AD si posiziona al di sopra della linea rossa tratteggiata, i valori di ritorno più bassi possono comunque essere utilizzati, mentre i valori di ritorno più elevati sono probabilmente inaffidabili.
In questo esempio l’errore quadratico medio per le intensità di 6 giorni corrisponde al valore critico. La statistica AD per le intensità di 6 giorni si situa al di sopra del valore critico. Perciò per questa durata occorre valutare accuratamente il confronto dei valori di ritorno stimati con le osservazioni. Bisogna inoltre tenere conto delle statistiche dei valori estremi dei cumuli delle precipitazioni su 6 giorni, se queste sono disponibili.
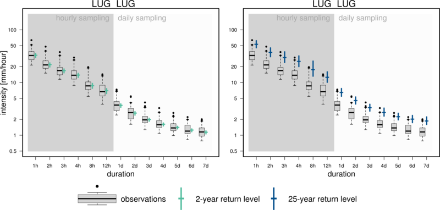
Il confronto dei quantili empirici con i valori di ritorno di 2 anni e 25 anni stimati consente di trarre conclusioni sulla qualità della stima per la fascia delle intensità già osservate. Nella stazione di Lugano il grafico delle intensità si basa su osservazioni orarie per 34 anni e osservazioni giornaliere per 50 anni. Poiché prendiamo in considerazione solo le massime annue, il valore di ritorno di 2 anni dovrebbe situarsi vicino alla mediana: il valore di ritorno di 2 anni dovrebbe quindi essere stato superato nella metà di tutti gli anni. Tuttavia ci aspettiamo che il valore di ritorno di 25 anni sia superato solo una o due volte durante l’intero periodo. In media l’evento dovrebbe perciò essere superato quasi 1,4 volte per ogni durata di 1 o più ore e circa 2 volte per ogni durata di 1 o più giorni. Per entrambi i periodi di ritorno il confronto con le osservazioni non mostra alcun comportamento anomalo evidente della stima.
Cosa fare se l’affidabilità del grafico delle intensità è insufficiente?
Ogni analisi dei valori estremi è sottoposta a un test di affidabilità e i relativi risultati sono indicati sulla pagina principale. Queste informazioni non valgono per l’incertezza della stima dovuta alla grandezza limitata del campione. Esse descrivono piuttosto la possibilità che le ipotesi su cui si basa la scelta del modello statistico possano eventualmente non essere pertinenti.
Se l’affidabilità è ad esempio dubbia, per un paio di durate il modello non rappresenta bene i valori estremi delle intensità delle precipitazioni osservati per alcune classi di durata. Si sono definiti tre classi di affidabilità: insufficiente, dubbia e buona. Nella tabella sottostante è indicato il significato di ogni livello e come comportarsi in ognuno dei tre casi.
Riassunto dell’affidabilità delle analisi dei valori estremi di diverse intensità
| Affidabilità | Interpretazione | Cosa fare? |
| insufficiente | Per alcune classi di durata delle precipitazioni i valori estremi osservati sono rappresentati male dal modello. | I valori di ritorno stimati non dovrebbero essere utilizzati. Per una prima impressione, utilizzate i box plot dei maggiori eventi osservati. Consultate le statistiche delle massime annue dei cumuli delle precipitazioni, se sono disponibili e affidabili. Se alcune delle classi di durate non presentano problemi, i valori stimati possono essere utilizzati provvisoriamente. Altrimenti occorre riferirsi alla stazione con dati affidabili più vicina. |
| poco affidabili | Per alcune classi di durata delle precipitazioni i valori estremi osservati non sono rappresentati bene dal modello. | È necessaria una valutazione accurata. Verificate la qualità della stima con gli strumenti ausiliari visivi disponibili. Se solo alcune intensità risultano di interesse, controllate se la durata desiderata presenta problemi evidenti. Se non è il caso, procedete come di consueto; altrimenti adottate le stesse misure come in caso di affidabilità insufficiente. |
| affidabili | Per la maggior parte delle classi di durata i valori estremi osservati sono rappresentati bene dal modello. | I valori di ritorno stimati possono essere utilizzati. Nel complesso le intensità massime annue delle precipitazioni sono ben rappresentate dalle distribuzioni stimate attraverso la maggior parte delle classi di durata . |