Navigazione veloce (Tasti accesso rapido)

Ambito dei contenuti

Circolazione generale dell'atmosfera - seconda parte

MeteoSvizzera-Blog | 17 novembre 2024
1 Commento

La rotazione terrestre è un elemento centrale necessario per spiegare la dinamica dell'atmosfera del nostro pianeta. Nel blog di ieri abbiamo esaminato il modo in cui il moto rotatorio viene spiegato in fisica, in particolare attraverso i concetti di “quantità di moto” e “momento angolare”. Nel blog odierno invece introduciamo i concetti di vorticità assoluta e vorticità relativa. Nel testo vedremo come questi concetti sono strettamente legati a una forza ben conosciuta, ovvero quella di Coriolis.

  • Tempo

Piè di pagina

Navigazione top bar

Autorità federali svizzereAutorità federali svizzere

Navigazione di servizio

Sui dizionari la "vorticità" (dall'inglese vorticity) è descritta come "la componente rotatoria di un elemento fluido".  In meteorologia questo termine è maggiormente utilizzato rispetto alla parola più semplice "vortice".  Il termine vorticità viene utilizzato ogni volta che si è confrontati con un moto rotatorio nell'atmosfera.

Su una giostra, ad esempio, sia che ci si trovi al centro sia che ci si trovi sul bordo, la vorticità è la stessa, poiché si compie un giro completo su se stessi nello stesso tempo (l'asse di rotazione della giostra è parallelo all'asse verticale del corpo); ciò che cambia, tuttavia, è la velocità di movimento intorno all'asse, che aumenta man mano che ci si allontana dal centro, come abbiamo visto nel blog di ieri. In meteorologia, la vorticità è convenzionalmente descritta come positiva quando il senso del moto è antiorario (circolazione ciclonica nell'emisfero settentrionale) e negativa quando il senso è orario (circolazione anticiclonica nell'emisfero settentrionale). Il suo valore aumenta in proporzione alla velocità di rotazione.

La Terra però non è una giostra (ovvero, non è un disco): è una sfera e questo fattore cambia le carte in tavola. Se vi trovate per esempio ai poli (nord o sud), l'asse di rotazione terrestre è parallelo all'asse verticale del vostro corpo. Se iniziate a spostarvi verso l'equatore invece, l'asse del vostro corpo non sarà più parallelo: l'angolo d'incidenza tra i due assi aumenterà graduealmente, raggiungendo il massimo (90°) all'equatore, ovvero i due assi risulteranno perpendicolari. In quella posizione, la vorticità risulterà pari a zero. In effetti, una persona che si trova all'equatore ruoterà attorno all'asse terrestre, ma non attorno al proprio asse. Riassumendo, più ci si allontana dal polo, più velocemente si ruoterà attorno all'asse di rotazione della Terra, e più lentamente attorno al proprio asse. E per le masse d'aria? Il ragionamento da fare è esattamente lo stesso.

Il legame tra vorticità e latitudine è descritto dalla seguente formula matematica:

Vorticità = 2ΩsinΦ (dove Ω rappresenta la velocità angolare della Terra e Φ la latitudine).

Poiché 2Ω è costante, si può notare che la vorticità dipende solo dalla latitudine. Questa formula è chiamata appunto “parametro di Coriolis”.

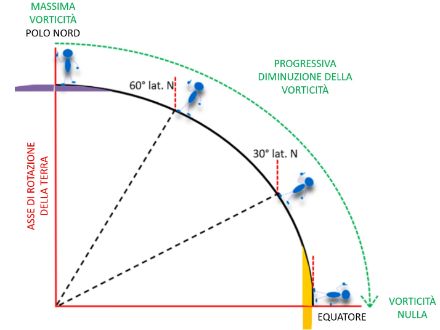
Dallo schema precedente si possono dedurre due fattori meteorologici molto importanti:

1. In prossimità del polo (diciamo entro un angolo di 20° da entrambi i lati), la vorticità è massima e varia poco perché la Terra può essere quasi comparata a un disco su queste distanze limitate (area viola sulla figura 1). D'altro canto, la quantità di moto delle masse d'aria è molto bassa perché sono vicine all'asse di rotazione.

2. In prossimità dell'equatore, la vorticità è praticamente nulla, ma la quantità di moto delle masse d'aria è elevata a causa della grande distanza che le separa dall'asse di rotazione terrestre (area evidenziata in arancione).

Queste considerazioni saranno essenziali quando esamineremo i movimenti latitudinali delle masse d'aria, cioè dall'equatore verso i poli e viceversa.

Vorticità planetaria, vorticità relativa e vorticità assoluta

Quando due o più elementi si muovono l'uno rispetto all'altro, per descrivere il movimento è necessario innanzitutto definire il quadro di riferimento dell'osservatore. Se l'osservatore è totalmente esterno agli elementi in movimento, il suo punto di vista è detto “assoluto”; se è legato a uno di questi elementi, ovvero l'osservatore si sposta "con l'elemento", il suo punto di vista è considerato “relativo”. Se per esempio state viaggiando in autostrada a 100 km/h da ovest a est in presenza di vento con raffiche di 40 km/h nella stessa direzione di marcia (ovvero vento da ovest), rispetto a voi il vento soffierà da est (frontale) con una velocità di 60 km/h (100 km/h - 40 km/h=60 km/h).

Supponiamo di essere in vacanza nel Parco Nazionale del Monte Kenya, situato esattamente sull'equatore, in una giornata soleggiata senza vento. Dal vostro punto di vista, la velocità della particella d'aria che vi circonda è pari a zero, eppure questa particella d'aria - legata alla Terra dalla forza di gravità - si sta muovendo nello spazio a una velocità di 1674 km/h.

Allo stesso modo, una massa d'aria completamente immobile al polo non vi sembrerà interessata da alcuna vorticità (ammettendo che fosse percepibile...), anche se essa compierà una rivoluzione completa su se stessa in 24 ore. Questa vorticità, che è interamente legata alla rotazione della Terra, è nota come vorticità “planetaria”.

Oltre alla vorticità planetaria, l'atmosfera in movimento può essere soggetta a vorticità legata al proprio spostamento. Questa vorticità è detta “relativa”, perché il punto di vista adottato è quello di un osservatore sulla Terra. Sono conosciuti due tipi di vorticità relativa:

1. Vorticità legata alla curvatura delle correnti atmosferiche: flusso ciclonico (vorticità positiva) e flusso anticiclonico (vorticità negativa):

2. In relazione alla velocità delle correnti atmosferiche. Una differenza di velocità all'interno di un flusso, anche se rettilineo, genera movimenti vorticosi, come mostrato nell'illustrazione seguente. Per verificarlo, mettete un piccolo pezzo di legno in un flusso (per esempio in un torrente con velocità laterale inferiore a quella centrale a causa dell'attrito esercitato dalle sponde) e vedrete che inizierà rapidamente a girare su se stesso:

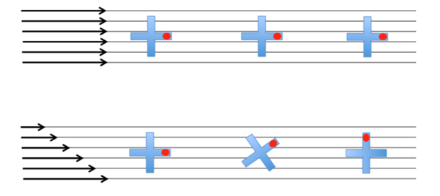
Sommando la vorticità planetaria (Vp) con la vorticità relativa (Vr) si ottiene la vorticità assoluta (Va), che può essere descritta con la formula seguente:

Va = Vp + Vr

La vorticità assoluta è l'insieme dei moti vorticosi così come verrebbero percepiti da un osservatore situato nello spazio. Come per il momento angolare, la vorticità assoluta di una massa d'aria è immutabile in assenza di influenze esterne; si dice dunque che è conservativa. Nel terzo blog di questa serie mostreremo come la circolazione generale dell'atmosfera è in gran parte determinata dalla necessità delle masse d'aria in movimento, verso i poli nel caso di aria di origine tropicale, o verso l'equatore nel caso di aria polare, di conservare questa vorticità assoluta.

Nei prossimi giorni abbiamo però in coda degli altri contributi da pubblicare. Attendete dunque qualche giorno!

Qui trovate un interessante esperimento (che potrete facilmente fare da soli) che illustra la vorticità in un fluido (purtroppo in inglese, ma abbastanza intuitivo).

Altri riferimenti:

- Circolazione globale dell'atmosfera - prima parte

- La forza di Coriolis

- Il vortice polare, l'ammistratore del freddo (#lameteospiegata)

Chi siamo

MeteoSvizzera è l’Ufficio federale di meteorologia e climatologia. Teniamo sotto controllo la situazione meteorologica 24 ore al giorno, per non lasciarvi mai senza una bussola affidabile, anche nei giorni con nebbia.

Informazioni su questo sito web