Navigazione di servizio
Ricerca
Immaginiamo una parata militare in cui i soldati passano davanti a noi in file da 20 perfettamente allineate. Al comando “quarto di giro a sinistra”, la truppa effettua un cambio di direzione di 90° a sinistra, mentre le file rimangono perfettamente allineate (e non è così semplice, come sa chi ha frequentato la scuola reclute). Cosa succede quindi? Il soldato all'estrema sinistra della fila farà un quarto di giro a sinistra rimanendo al suo posto, mentre il soldato all'estrema destra della fila dovrà accelerare notevolmente il passo per rimanere in linea con gli altri soldati. Quindi, per una rotazione dello stesso angolo di 90°, la distanza da percorrere sarà sempre maggiore quanto più ci si allontana dall'asse di rotazione rappresentato dal 1° soldato sull'estrema sinistra; ma poiché questa distanza deve essere percorsa nello stesso tempo da tutti i soldati (per non deformare la linea), la velocità (detta velocità lineare) aumenta proporzionalmente quanto più ci si allontana dall'asse.
Questo esempio mostra che una velocità di rotazione non può essere espressa in termini semplici e usuali, come km/h, ma deve essere espressa includendo l'angolo percorso. In questi casi si parla di velocità angolare, cioè dell'angolo percorso per unità di tempo; in fisica è indicata con il simbolo Omega (Ω). Ci sono molti modi di esprimerla, dai più semplici (radianti/secondo, per esempio) a quelli più diretti, come i giri al minuto della cyclette o del motore dell'auto.
Siete ancora qui? Andiamo avanti...
Prendiamo l'esempio della Terra, il cui movimento è in realtà piuttosto complesso nei dettagli, ma può essere semplificato come segue: ruota due volte più lentamente della lancetta del vostro orologio, poiché compie un giro su se stessa in 24 ore (quindi Ω = 360°/24h). Ai poli, la velocità lineare reale di una persona sarà pari a zero, poiché girerà su se stessa; all'equatore invece, e sapendo che il raggio della terra è di 6378 km, la velocità sarà di 1674 km/h e la distanza percorsa in 24 ore di circa 40.000 km. Non è poco...
Quantità di moto e momento angolare
Se una mosca si muove a 30 km/h, o se si tratta di un vagone FFS a pieno carico, si può intuire che non è la stessa cosa (ci si può anche mettere sulla traiettoria del vagone per verificare di persona). La differenza sta nella cosiddetta quantità di moto, cioè il prodotto di una massa (nota come m) per la sua velocità (nota come v). La quantità di moto di un vagone che viaggia a 30 km/h è quindi infinitamente maggiore di quella di una mosca che vola alla stessa velocità.
Come abbiamo visto nel capitolo precedente - e per una data velocità angolare - la velocità lineare effettiva di un oggetto in rotazione dipende dalla sua distanza dall'asse di rotazione. La quantità di moto dell'oggetto (che comprende la sua velocità) varia quindi anche in funzione della sua distanza da questo asse (il raggio, noto come r): chiamiamo “momento angolare” (o momento angolare) - noto come L - il valore che include questo parametro r nella quantità di moto, cioè il prodotto della quantità di moto e della distanza dall'asse di rotazione (L = mvr).
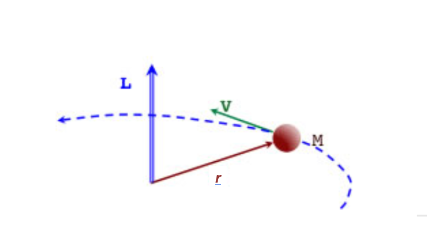
Se non è coinvolta una forza esterna, il momento angolare di un corpo non cambia. L'uguaglianza L = mvr significa quindi che se uno dei tre parametri m, v o r diminuisce, un altro di questi stessi parametri deve aumentare della stessa quantità affinché il momento angolare L rimanga invariato.
L'illustrazione più classica della conservazione del momento angolare è la velocità di rotazione di una pattinatrice artistica (in questo caso Denise Bielmann); questa velocità aumenta quando la pattinatrice avvicina le braccia al corpo. In linguaggio matematico, diremmo che diminuisce r (il raggio) e quindi v (la velocità di rotazione) aumenta, cosicché L (il momento angolare) si conserva.
Provate voi stessi utilizzando un semplice (ma ben oliato!) sgabello girevole: sedetevi sullo sgabello e girate il più velocemente possibile con le braccia e le gambe distese, poi riportatele gradualmente verso di voi. In questo caso la massa m rimarrà costante e la velocità di rotazione v aumenterà immediatamente, come per magia.
Un altro semplice esperimento consiste nel far ruotare un oggetto attaccato a una corda intorno al dito. Man mano che la corda si avvolge intorno al dito (il raggio r diminuisce), la velocità dell'oggetto aumenta.
E che dire della meteo?
Poiché la velocità angolare della Terra è costante, il movimento delle masse d'aria sulla superficie del globo è influenzato dal fatto che esse si muovono verso o lontano dai poli (cioè diminuiscono o aumentano la loro distanza dall'asse di rotazione r). Tuttavia, non dimentichiamo che la Terra è una sfera e non un disco, il che complica un po' le cose.
Non vi è chiaro? Non preoccupatevi, ritorneremo sul tema nella seconda parte di questo blog dedicato alla circolazione atmosferica!