Navigazione di servizio
Ricerca
Provate ad immaginarvi la seguente situazione: vi trovate ad un aperitivo, l'atmosfera è rilassata e le persone chiacchierano piacevolmente. All'improvviso qualcuno se ne esce con uno dei seguenti termini: "matematica", "fisica" oppure, ancora peggio "stocastica". L'atmosfera cambia improvvisamente: cominciate a sudare freddo. "Quantile", "mediana", "deviazione standard" e avete definitivamente soffocato qualsiasi conversazione... A meno che non stiate conversando con una persona appassionata fruitrice dei nostri blog. Eppure la matematica è in realtà molto semplice. Ammettetelo: chi di voi non ha calcolato la propria media dei voti quando andava a scuola?
Probabilmente non è impossibile che...
Sicuramente ve ne sarete accorti: Le previsioni del tempo, un tempo puramente deterministiche (ci sarà questo o quel tempo), vengono sempre più frequentemente formulate utilizzando termini probabilistici come "possibile", "probabile", "non escluso", ecc. Nei grafici, ad esempio, non viene fornito solo un (singolo) valore deterministico della temperatura, ma anche un intervallo di temperatura previsto.
Meteo e probabilità
Il tempo segue un sistema caotico, che i modelli meteorologici cercano di descrivere attraverso innumerevoli formule matematiche.
Funzionamento di un modello di previsione numerica (in breve): lo stato iniziale dell'atmosfera viene determinato attraverso il maggior numero possibile di dati di misura (misure al suolo, radiosondaggi, dati radar/satellitari...) e il modello meteorologico viene inizializzato con questi dati. Il modello meteorologico calcola quindi il tempo previsto per i giorni successivi. Fin qui tutto bene, siamo di fronte a una singola soluzione, cioè a una previsione deterministica.
Torniamo al nostro tempo caotico: è ovvio che, nonostante tutti gli sforzi, lo stato iniziale del tempo non potrà mai essere completamente catturato dalle misurazioni. Già all'inizio del nostro modello meteorologico dobbiamo fare i conti con le incertezze che si "propagano" con il tempo di previsione.
Le incertezze nelle previsioni meteorologiche sono stimate con il metodo dell'ensemble. Il modello viene eseguito più volte, ogni volta con condizioni iniziali leggermente diverse. Ogni calcolo del modello fornisce una previsione meteorologica, più precisamente un "membro". Successivamente, tutti i "membri" vengono confrontati tra loro e valutati. È qui che entra in gioco il calcolo delle probabilità, e che introduciamo i termini più importanti come "media", "mediana", "quantile".
Definizione dei termini
Più volte al giorno, il modello ECMWF IFS produce 51 previsioni a 10 giorni, modificando leggermente le condizioni iniziali. Queste 51 diverse previsioni sono chiamate "membri", come descritto sopra.
Per una data località, osserviamo di seguito le precipitazioni previste nelle 24 ore per un dato giorno. Supponiamo ora che la distribuzione delle precipitazioni in base ai diversi "membri" sia la seguente (rappresentazione idealizzata per una migliore comprensione):
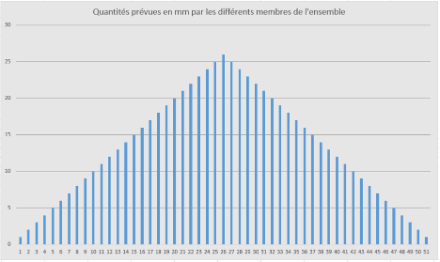
Si può notare che la distribuzione delle precipitazioni è uniforme e simmetrica intorno al valore massimo di 26 mm, che è rappresentato dal "membro" n. 26.
Per illustrare meglio i vari termini statistici, è utile disporre prima i valori dei singoli "membri" in ordine crescente (questa è chiamata "funzione di distribuzione cumulativa"), il che porta alla seguente rappresentazione. Vediamo che ogni valore è mostrato due volte e il valore massimo (che si verifica una sola volta, vedi grafico precedente) è 26 mm.
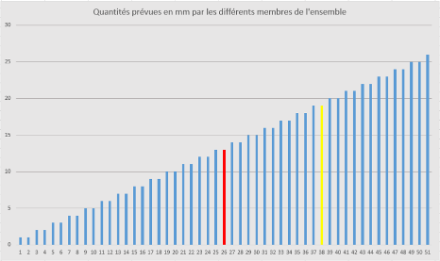
Sulla base dell'esemplare distribuzione delle precipitazioni dei 51 "membri", passiamo ora ai termini statistici più importanti:
- La media è il termine più semplice. Si determina sommando i valori di tutti i membri e dividendoli per il numero di membri. Si tratta quindi di un singolo valore la cui rappresentatività rispetto all'insieme può variare notevolmente (cfr. deviazione standard). Nella distribuzione sopra riportata, il valore medio è di 13 mm ed è rappresentato dal "membro" n. 26 (in rosso).
- La deviazione standard rappresenta la diffusione dei valori intorno alla media. In pratica, ci dice quanto la media sia rappresentativa del campione. Più piccola è la deviazione standard, più significativa è la media. Nella distribuzione sopra riportata, la deviazione standard è di 7,4 mm, il che significa che la media di 13 mm non è molto rappresentativa dell'insieme. In generale, si può affermare che maggiore è la deviazione standard, minore è la certezza della previsione.
- La mediana è il valore che divide il campione esattamente a metà, ovvero una metà dei membri con più precipitazioni e l'altra metà con meno precipitazioni. Poiché la distribuzione in questo esempio è simmetrica, la mediana corrisponde al valore medio ed è rappresentata anche nel grafico precedente dal "membro" n. 26 con 13 mm (in rosso). Se la distribuzione non è simmetrica, la media e la mediana di solito non sono congruenti.
- I quantili sono percentuali (solitamente standardizzate) che riassumono un certo numero di membri. Ad esempio, il quantile del 75% (rappresentato dal "Membro" n. 38 (giallo), 19 mm nel nostro esempio) ci dice che il 75% dei "Membri" si aspetta meno di 19 mm e il 25% dei "Membri" simula più di 19 mm. Si noti che la mediana non è altro che il quantile del 50%; il quantile 0% rappresenta la previsione con meno precipitazioni e il quantile 100% rappresenta l'estremo opposto.
Le probabilità di superare/scendere al di sotto di valori soglia predefiniti possono essere calcolate a partire dai "membri". A MeteoSvizzera, le probabilità sono utilizzate principalmente nel contesto dell'allertamento.
Esempi concreti
Nel mondo reale la distribuzione delle precipitazioni non è mai simmetrica. Per il nostro comune di esempio, la distribuzione delle precipitazioni appare come nel grafico seguente. Molti "membri" non simulano alcuna precipitazione, mentre pochi "membri" danno luogo a molte precipitazioni.
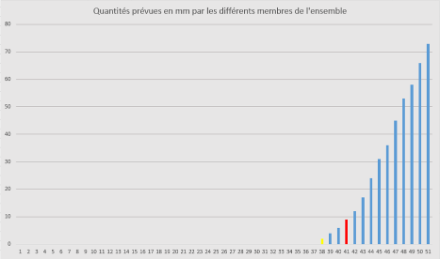
- Media: 9 mm (in rosso).
- Deviazione standard: 19 mm
- Mediana ("Membro" n. 26): 0 mm
- 75mo quantile: 3 mm (in giallo).
In questo esempio si nota subito che il valore medio di 9 mm non è rappresentativo, poiché la grande maggioranza dei "membri" non prevede precipitazioni (la deviazione standard, tra l'altro, è molto ampia). Ci rendiamo anche conto che la mediana e la media non hanno lo stesso valore perché la distribuzione dei membri non è simmetrica. In questo caso, la mediana - con il valore 0 mm - fornisce un'indicazione utile, poiché è identica per la grande maggioranza dei "membri".
Il valore di 3 mm per il quantile del 75% indica che solo il 25% delle membrature fornisce più di 3 mm di precipitazione. Da ciò si può concludere che è molto probabile che la località in questione non riceva precipitazioni o ne riceva poche. Ma non si escludono nemmeno 70 mm di precipitazioni.
L'esempio seguente mostra la distribuzione "fittizia" delle precipitazioni dei nostri 51 "membri" durante il passaggio di un fronte quasi-stazionario:
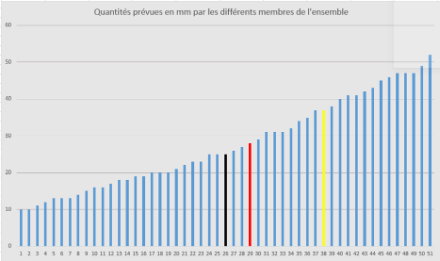
- Media: 28 mm (rappresentata dal "Membro" n. 29 in rosso).
- Deviazione standard: 12 mm
- Mediana: 25 mm (in nero).
- 75mo quantile: 37 mm (in giallo).
In una situazione come questa, la probabilità di precipitazioni è molto alta, ma c'è molta incertezza sui totali esatti, dato che la differenza tra i due estremi è di oltre 40 mm. La deviazione standard, tra l'altro, è significativa: 12 mm. La distribuzione è abbastanza simmetrica, la media e la mediana sono molto vicine tra loro. In un esempio del genere, ci si potrebbero aspettare 20-30 mm di precipitazioni.
Utilizzo delle probabilità a MeteoSvizzera
Analizziamo ora la previsione del modello COSMO-2E con 21 "membri" per il totale delle precipitazioni delle 24 ore tra martedì 4 luglio e mercoledì 5 luglio alle 18 UTC, utilizzando i vari termini statistici citati.
Il valore medio non è interessante per le previsioni di precipitazione perché è sempre diverso da zero non appena le precipitazioni sono presenti, anche se solo in un singolo membro; pertanto non viene utilizzato. La deviazione standard, invece, è importante perché ci dà un'indicazione dell'affidabilità della previsione.
I 21 "membri"
Si tratta di 21 previsioni diverse, per la stessa data e lo stesso parametro, partendo da condizioni iniziali leggermente diverse:

La mediana
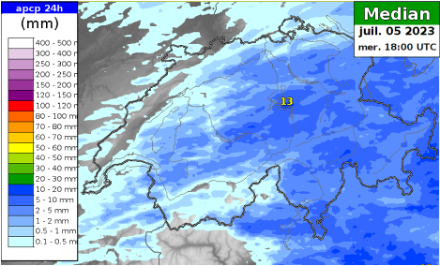
La deviazione standard

La mappa della deviazione standard ci mostra che le quantità attese nella Svizzera centrale e nel vicino territorio di Glarona, nonché in Ticino, compreso il Moesano e la Val Calanca, sono molto incerte, a seconda della regione tra più o meno 5 e 20 mm.
I quantili

Le probabilità

Nelle situazioni temporalesche, le probabilità sono generalmente basse perché la distribuzione abbastanza casuale delle precipitazioni rende improbabile che grandi quantità di precipitazioni si verifichino nello stesso punto in tutti i "membri" dell'ensemble.
Probabilità in un punto
Per un determinato punto (in questo caso Aigle, VS) le probabilità appaiono come mostrato di seguito. I quantili 0 e 100 % sono rappresentati da barre verticali, i quantili 90-75 % e 10-25 % da stretti rettangoli blu chiaro, il quantile 25-75 % da un ampio rettangolo blu scuro e la mediana da una linea nera orizzontale. In generale, più ampia è la "scatola" blu, maggiore è la dispersione e l'incertezza della previsione.
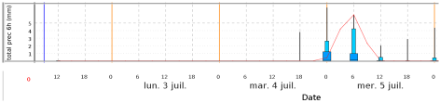
Da questo esempio notiamo che il rischio di precipitazioni cambia in incrementi di 6 ore. Per Aigle, il rischio di precipitazioni è massimo nella notte tra martedì e mercoledì, dalle 18.00 alle 00-06 UTC. Per il periodo 00-06 UTC, il quantile 100% dà 6 mm, il quantile 90% dà 4 mm, il quantile 75% dà 1 mm e la mediana dà 0,01 mm.
Conclusione
Mentre i "membri" della previsione d'insieme hanno un'elevata coerenza meteorologica perché seguono uno scenario specifico, questo non è vero per i valori derivati come la mediana, il quantile, ecc.
Ad esempio, la mappa del quantile di precipitazione del 100% mostra il valore di precipitazione più alto per ogni pixel, indipendentemente dagli scenari meteorologici che hanno causato questo valore. Pertanto, lo scenario che produce la massima precipitazione a Ginevra non è necessariamente lo stesso che produce la massima precipitazione a Zurigo. Eppure sono entrambi sulla stessa mappa; lo stesso vale per la media o la deviazione standard.
Come possiamo vedere, le'approccio probabilistico è molto importante per le moderne previsioni meteorologiche. Le previsioni probabilistiche sviluppano tutto il loro potenziale solo se abbinate ad approcci più classici, come quello climatologico e l'esperienza umana (conoscenza del terreno e dei punti di forza e di debolezza dei vari modelli). È qui che entriamo in gioco noi previsori/e...